Warning: this post has real math for the nerds who like that stuff. Like the for-realsies stuff. Not into a ton of math? Skip to the TL;DR section near the end.
So here's a question: how many matches, on average, does it take to progress upward in the Victory track? Let's say you're starting off in the Bronze track, and it takes two trophies to advance from B3 to B2. How many matches would it take to win those two trophies? Let's say your average win percentage is 50%: on average, you win about half your matches. You might think the average number is four: it takes, on average, two matches to win a trophy, so it should take four matches to win two.
The problem is the mechanics of advancement. When you win you earn a trophy, But when you lose, you lose one. So while yes, it will take on average four matches to win two in a row, winning two in a row is not the only way to earn two trophies. You could win, lose, win, then win. Or you could lose, win, lose, lose, lose, win, lose, win, win. Each of these sequences of wins and losses has a certain chance of happening. How do you add them all up and somehow average them out? The answer is you don't. Instead, we're going to use some advanced math techniques. These are advanced in the sense most people who don't do math for a living never encounter them, but they are common mathematical tools to solve problems like this. I'm going to try to explain them as simply as possible.
If you're in Bronze, there are three possible situations you could be in. You could have zero trophies. Or you could have one. Or you could have two. Let's call this T0, T1, and T2. And for each of these situations, there is the number of matches (on average) you will need to complete the tier. We'll call these numbers S0, S1, and S2.
Now, if you are in T2, what is S2, the number of matches you need to do to reach the top of your current tier? Answer: zero. You're already there (in-game you will only be in this state briefly, and then get pushed up to have zero trophies in the next higher tier, but this is for completeness sake). Easy enough. But what if you are in T1 and you only have one trophy? What is S1, the number of matches on average to reach T2 (the end)? Well, we know that you will need at least one more match, because you aren't there yet. And after that match, you will either win or lose (theoretically speaking, it is possible to tie, but we'll consider this a sufficiently rare event to not matter here). If you win, you will go from T1 to T2. If you lose, you will go from T1 to T0. The odds of going to T2 are p, where p is your win percentage. The odds of going to T0 are (1-p), which is your chance to lose. If you go to T2, the amount you need after that is S2, which we already said was zero. So we can say that if you are in T1, then S1, the average number of matches you have left to go is:
S1 = 1 + p*S2 + (1-p)* S0
We can do the same for T0, the case where you have zero trophies. In exactly the same manner as before, we can say that T0 requires at least one more match, and after that match you will be in either T1 if you win, or back to T0 if you lose (because you cannot backslide). So then:
S0 = 1 + p*S1 + (1-p) * S0
We also know S2 = 0, because that's the end, so we have three equations:
S2 = 0
S1 = 1 + p*S2 + (1-p)* S0
S0 = 1 + p*S1 + (1-p) * S0
We can now substitute S2 into the equation for S1 and end up with an equation with two variables, S1 and S2. We can then solve for S1 in terms of S0 and substitute into the equation for S0 and get an equation with only S0 and p. Skipping the algebraic substitution, we get:
S0 = (2-p)/p
Now we can plug in p= 0.5, and get S0 = 3. Intuitively this might make sense: if it would take four matches to get two in a row, and there are other ways to get two trophies, the average has to be lower than that (because having other ways means it has to be easier than if that was the only way). However, that intuition isn't actually correct, as later calculations will show. These kinds of situations are very deceptive when it comes to normal intuition.
Let's move on. Silver through Diamond require having three trophies instead of two. Using the same logic as above, we can see there will be four possible states, T0, T1, T2, and T3, and each state has an average number of matches to reach the end from that point, S0, S1, S2, and S3. Each state has a probability p of moving forward and (1-p) of moving backward, with two exceptions. T3 is the end, and you cannot move backward from T0, you just stay there. Mathematicians would generally call this a Markov chain, for those interested. We tend to draw them something like this:
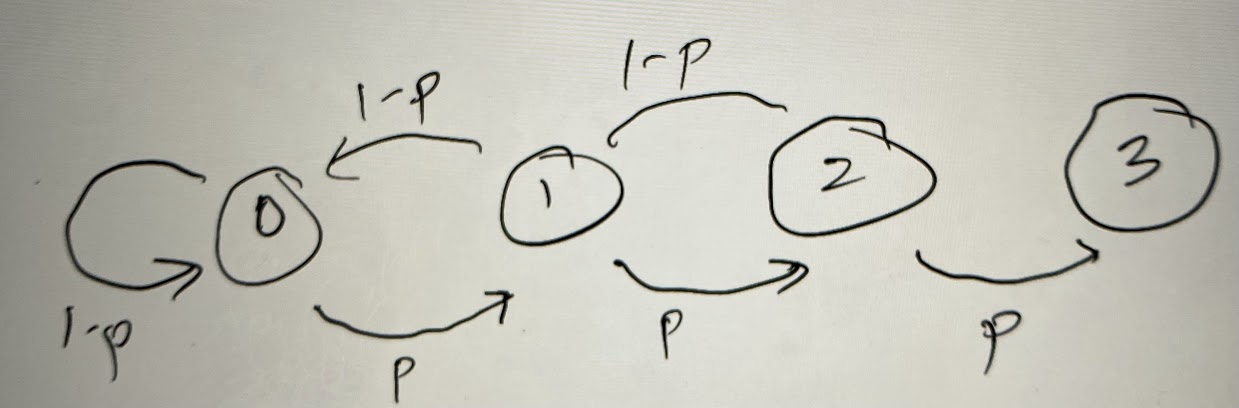
And then we can write our state defining equations based on that diagram like so:
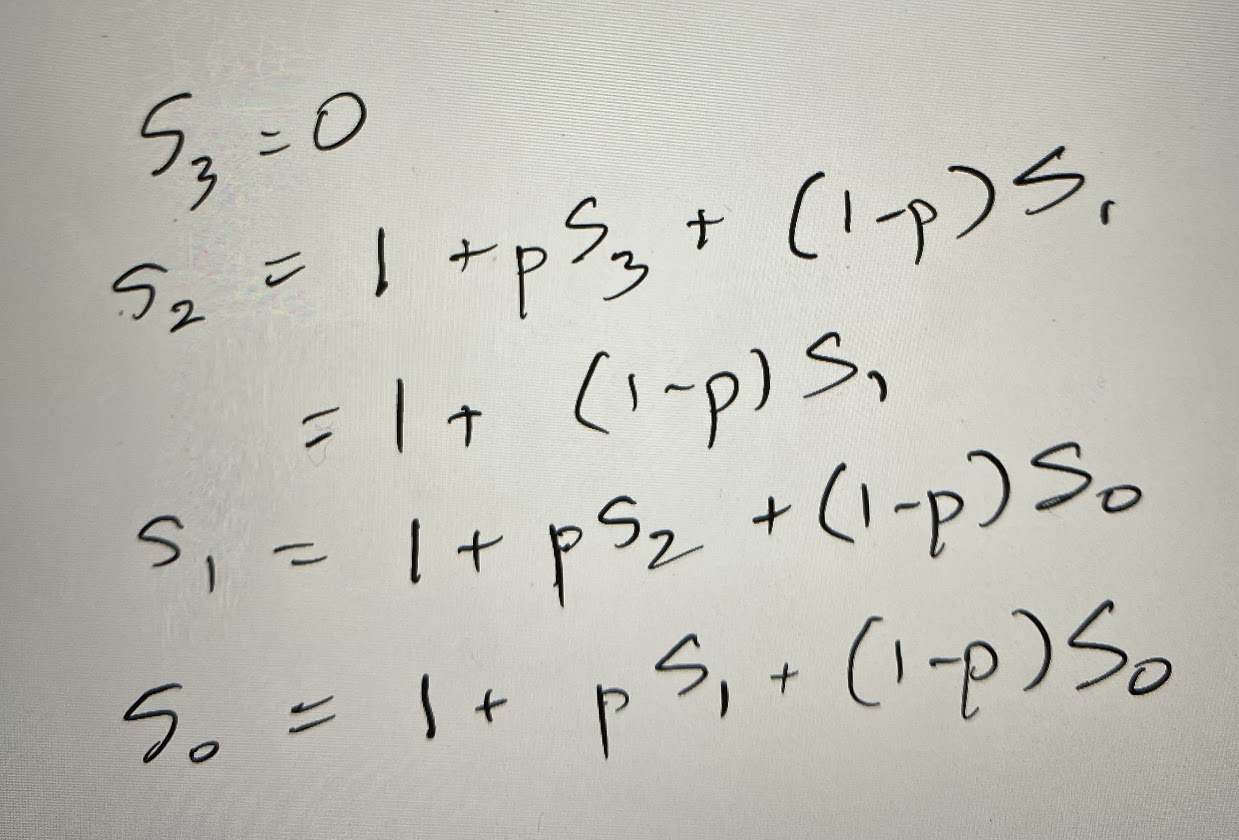
And then if we start substituting, substituting, and more substituting, and we eventually get:
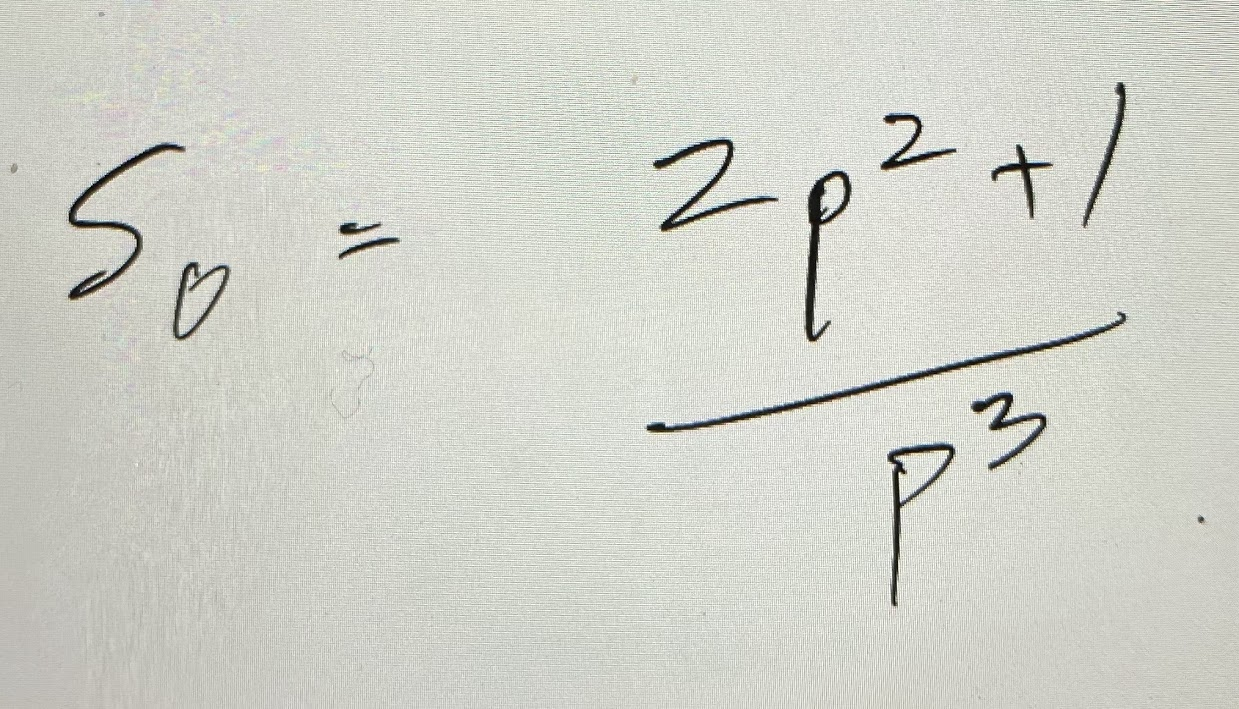
If we plug in 50% (0.5) we get 12. So it takes, on average, 12 matches for someone who wins at a 50% rate to string together enough wins to reach three net trophies [note: this is more than the naïve guess of eight, which shows intuitive guessing for these situations doesn't always work].
Incidentally, I mentioned I'd be using some advanced math techniques. The first one is Markov analysis, as shown above. The second one is a subtle and underappreciated one. When you don't know the answer to a mathematical question, a very common, but often overlooked technique is to *assume* you know the answer, give it a name, and then see what properties this thing would have, if you knew it. This allows me to just say the answer to the question is S0, and then create equations using S0 as if I knew them, and then use those equations to determine what S0 must be, to satisfy all those constraints. It is the advanced inductive version of "Solve for X" in high school math.
This just leaves Vibranium. Vibranium requires five trophies. Using the same technique, we can set up the Markov state chain, along with the state equations:
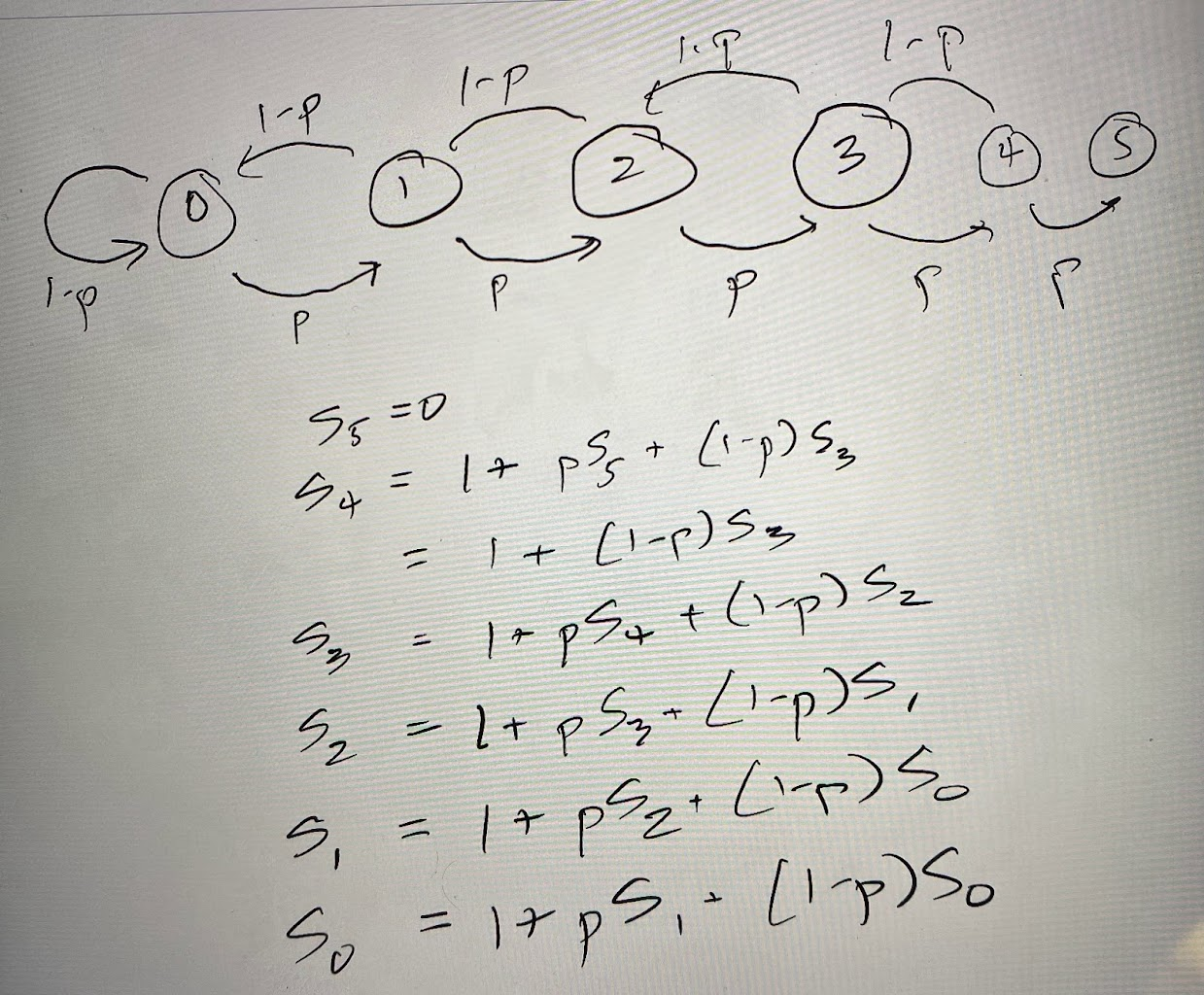
And then we can just solve for S0 using substitution:

You know what? Let’s leave that as an exercise for the reader. Yeah, I can’t have all the fun. Let’s just take those state equations and plug in a few values for p: 50%, 75%, and 33%. While we are at it, let’s calculate how many matches to promote one tier within each bracket from Bronze to Vibranium:
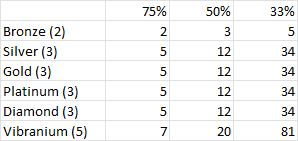
So this is the average number of matches a player would have to play to get enough trophies to advance, for two trophies, three trophies, and five trophies. To calculate how many matches it would take to promote from one tier to the next, we have to account for the fact that it takes two promotions to reach the top Bronze (you start automatically on B3, and you have to promote to B2 and then to B1) but three promotions to reach the top of silver through Diamond. Vibranium require just one promotion. So the total number of matches, on average, to reach the top of each tier is:
[TL;DR readers should jump to here]
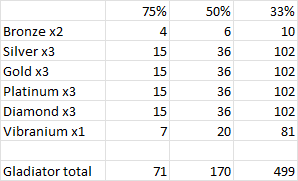
If your win percentage is 75% or better, promotion is likely to be a relatively straight forward process. But at 50% it starts looking like a pretty significant chore. At 33% it’s approaching hopeless without expending ludicrous amounts of effort (or getting extremely lucky).
In theory, matching by ELO (rating) seeks to find even matches for opponents: the goal is to achieve a roughly 50% win rate for most competitors, because the intent is to match players of comparable win percentage. Eventually winners face winners and things roughly equalize. Every beta of Battlegrounds used an ELO based match system. However, the current system appears to use a match system that heavily weights roster/deck strength. This means there’s no attempt (or at least a difficult to notice one) to match equally strong players in terms of win rate. Instead, if you have a stronger roster than players of comparable skill, you have a permanent disadvantage in Battlegrounds, because you’ll tend to get matched against players of higher skill. Conversely if you have a weaker roster than players of comparable skill, you have a permanent advantage in Battlegrounds, because you’ll tend to get matched against players of lower skill. This means there’s no reasonable assumption that players can expect to win about 50% of matches. Instead some players are likely to get far higher win rates, owing to their high skill (relative to roster strength). Conversely there must be players that will experience significantly lower than 50% win rates, likely semi-permanently.
What this means for the player experience in Battlegrounds is probably not super-positive. If a player is never going to make it into the Gladiator tier, that’s one thing. Not everyone belongs there. But if many players find they cannot advance at all, if they discover that track progression quickly stalls out and the rewards for promotion are more or less permanently out of reach, I would assume the long term impact of this would be to deter most players from participating on anything other than a very casual level. Whether that's an issue, or a desirable feature is an open question. On the one hand, the mode does
heavily favor higher skill players - at least on a relative basis. That's not a bad thing for a competitive game mode. But if it also discourages participation for all but the highest skilled players across differing roster strength, that does not bode well for a game mode that requires a minimum density of players entering the turnstile for the match maker.
PS: this is a lot of math, and I'm not as sharp as I used to be, so I double checked my calculations with Wolfram Alpha where possible. This is WA double checking my three trophy algebra:
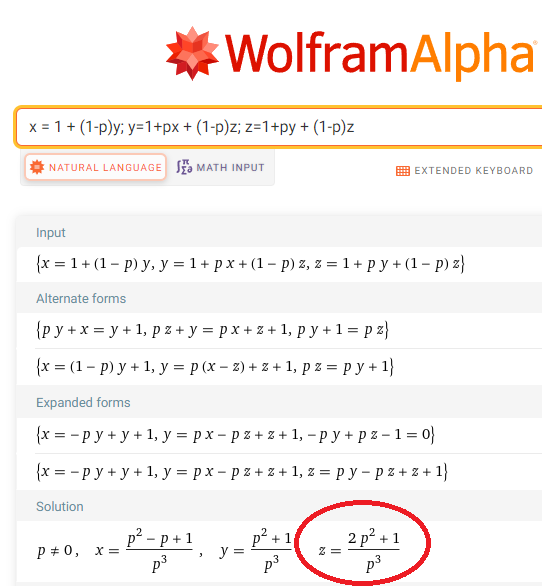
But there's still always the chance for an error. If anyone wants to double check any of this, by all means have at it. I welcome any corrections to errors someone might be able to spot. Good luck using WA/Mathematica to find the closed form solution to Vibranium, however. Unless you're a Mathematica god, you aren't going to get the result you are hoping for.