So I finally ended my run on the current featured 6* crystal today, when I pulled the last thing I was hunting for (OG Scarlet Witch) on pull #69. This is
by far the most featured crystals I've ever opened for one version, fueled by my ludicrous pursuit of Scarlet Witch and the fact that 6* shards are just a little too available in a little too many game modes for my own sanity.
Sixty nine crystals sounds like a lot, but it actually isn't a statistically significant amount if you are trying to, say, prove that every drop has an equal chance of falling. You'd need tens of thousands of crystals to do that. It is enough to demonstrate that most of the silly conspiracy theories are just that: silly. Here's my overall distribution of drops:
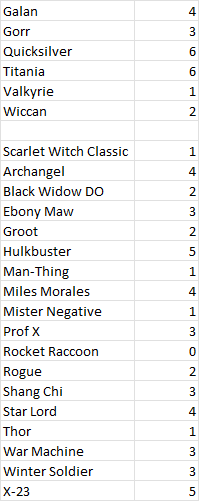
Out of 69 crystals, 22 were featured drops. The statistical average would be about 17 (69/4). So the crystal isn't significantly biased away from the new featured champs. There's not enough data to prove they are *exactly* balanced, but they are statistically unlikely to be biased low. If I should normally get 17 and I actually got 22, that might be lucky. But if someone thinks they are biased in such a way so that featureds come up, say, half as often as they should, then I got 22 when the crystals are rigged to generate something closer to 8. That's very, very unlikely.
69 crystals isn't enough to show that any one particular drop lands statistically at the presumptive percentage, but is it enough data to show *anything* statistically interesting? As it turns out, it is. We can analyze whether the crystals roughly follow gatcha math. What do I mean by that?
Gatcha mechanics generally refers to the situation where a person/player is confronted with an opportunity to get a random reward, selected from a set of rewards, where the presumptive desire is to collect the entire set (or some desirable subset of the set). Now, most people don't actually try to get all 24 champions in the featured crystal (if for no other reason than most people tend to have some of them already), but what if I analyze the data *as if* I was trying to collect them all. Is there enough data to see if the crystal's random drops roughly follows what I would expect? In at least rough terms, it is.
Let's answer one question first. If you were trying to get at least one of all twenty four champions from the crystal, about how long would that take? This isn't math that is often discussed. You might think you could calculate the odds of pulling the first champ, then the odds of pulling the second champ, and so on. But that doesn't work. While trying to pull the fifteenth champ, you might pull the eighteenth champ first, out of order. Then the math vastly overestimates how long it takes. But as it turns out, there is a relatively simple way to calculate this. We look at the average number of pulls it takes before you pull a champ you haven't pulled yet. If we go step by step, the answer drops out naturally.
We start with no champs and no crystals. How many crystals will it take before we pull a champ we haven't pulled yet? Obviously: 1. Whatever is in that crystal, it is guaranteed to be a new pull. Okay, we have one champion. Now how long will it take to pull a new champ? Well, 23 of the 24 champs would be new, and one would be a dup. If it were 12 new champs out of 24, the odds of pulling a new champ would be 50% - 12/24. And the number of crystals we would need to pull, on average, before we got a new champ would be 2, basically the reciprocal of the odds of a new champ. It is pretty obvious when the numbers are easy. But we generalize this for all situations: the odds of pulling a new champ are X/24, where X is 24 minus the number of new champs you have so far. And the average number of crystals you would need to open to get a new champ is the reciprocal of that, or 24/(1-new).
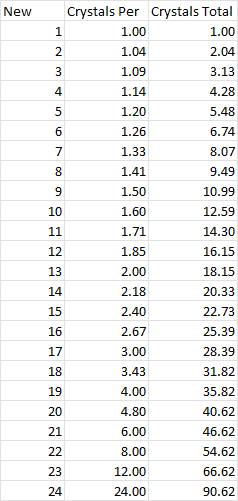
So to get one new champ it would take 24/24 crystals. To get two new champs would take 24/24 + 24/23 crystals. To get three new champs would take 24/24 + 24/23 + 24/22 crystals, and so on. We get this table:
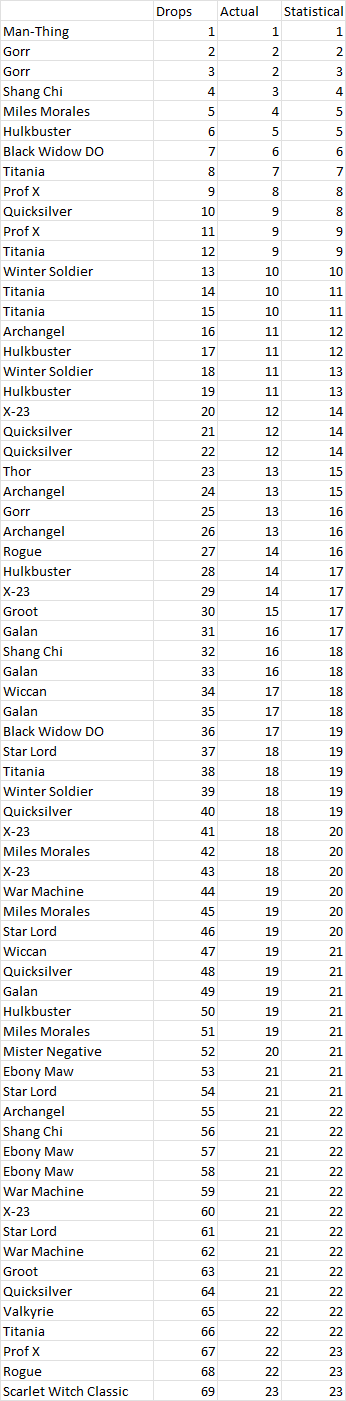
Now these are all my drops:

And this is a table of how many new champs I had, alongside the statistical average expected:
And how close was my distribution to the predicted gatcha new drop rate?
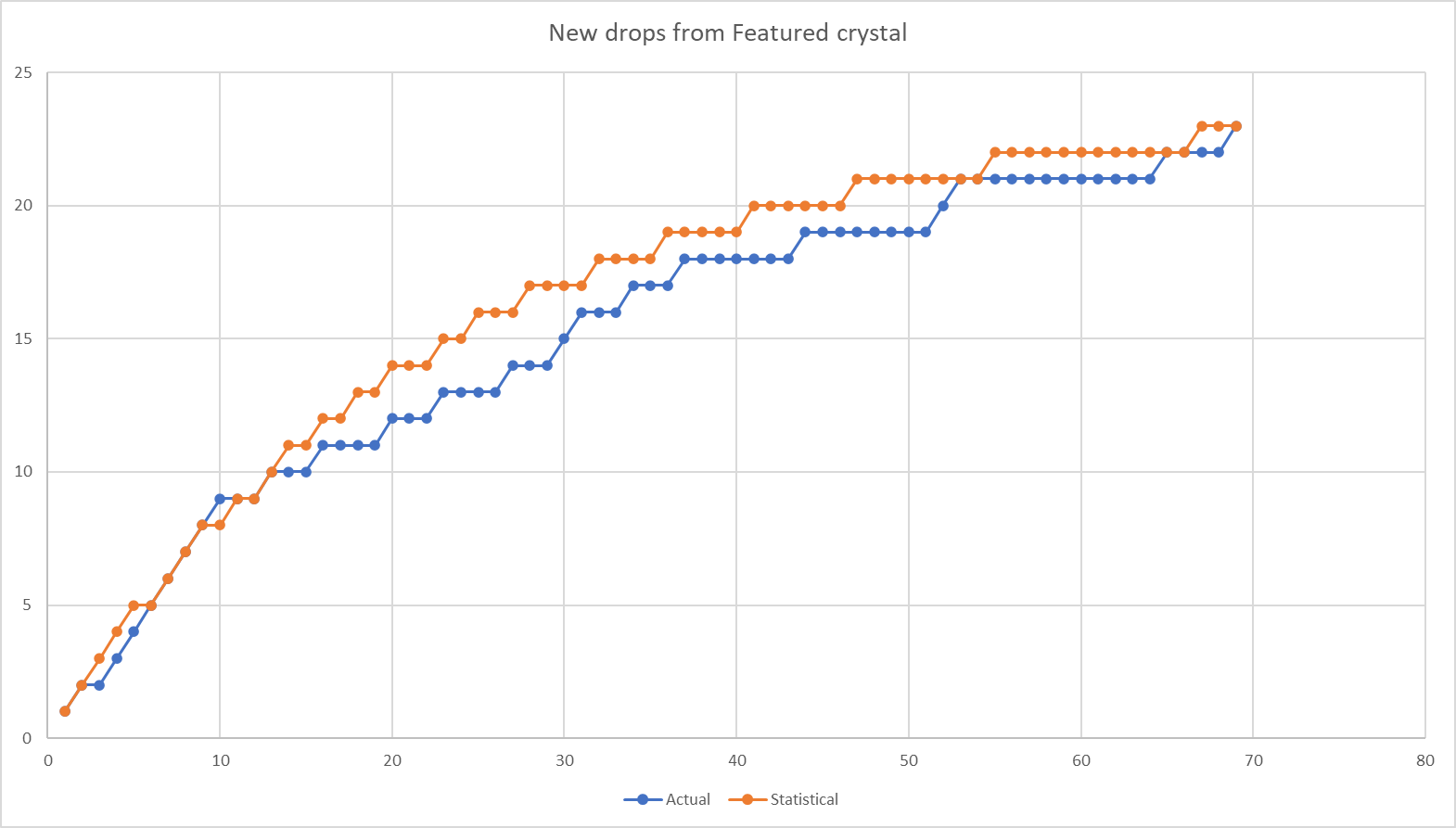
Pretty close. The crystal behaves, over long stretches, about as you would expect if each drop was roughly identical in drop rate. Now, this doesn't *prove* they are all identical in drop rates. It just shows they behave *like* they would. This means certain kinds of "rigging" are unlikely, in particular while it is statistically possible for some champs to be more likely than average, it is not statistically likely that some champs are far less likely than average. More likely champs would show up earlier, which would show up in the data as the blue line starting off higher than the orange line on the left side of the chart. But champs that were deliberately made much rarer would cause the blue line to drop progressively much lower than the orange line as you went to the right. That doesn't appear to be the case.
In other words, if Groot was twice as likely as every other champ, this sort of analysis wouldn't catch that (although the fact that I only pulled Groot twice would strongly contradict that conjecture). But if, say, all of the featureds were half as likely to show up, that *would* tend to show up here.
The last new champ I pulled was Scarlet Witch, which was the 23rd "new" champ I received from the featured crystals. Statistically speaking, #23 should have arrived on pull #67. It actually arrived on pull #69, which in statistical terms is basically a bullseye. The one champ I never pulled from the featured was Rocket Raccoon. Statistically speaking, I should expect him to show up around crystal #91, or 22 crystals from here (in actuality, I should expect it to take on average 24 crystals from here, because at this point I would be trying to get one out of 24 champs in the crystal, but this opens a different can of statistical analysis worms).
Oh hell no, I'm not opening 24 more featureds to see when Rocket Raccoon shows up.